Kansas Geological Survey, Open-file Report 96-46
by
Kristen L. Stanford, James J. Butler, Jr., Carl D. McElwee, and John M. Healey
KGS Open File Report 96-46
Presented at the AGU Fall Meeting, December 1996.
At sites of suspected ground-water contamination, slug tests are often performed in wells screened across the water table. Currently, there is considerable uncertainty regarding how to perform and analyze slug tests in this configuration. A field investigation was recently undertaken to develop a set of practical guidelines for slug tests in such wells. Tests were performed at three sites of moderate to high hydraulic conductivity. The results of this investigation can be summarized as follows: 1) the sufficiency of well development, potentially the most critical component of a test program, should be based on repeat slug tests and not the clarity of pumped water; 2) the water table can be considered a fixed boundary and the unsaturated zone can be ignored in most cases; 3) the effective casing radius should be based on a mass balance and not nominal screen dimensions; and 4) water-table fluctuations through time can be exploited to obtain some insight into the nature of vertical variation in K at a well. The major conclusion that can be drawn from this study is that conventional techniques for the analysis of slug-test data (e.g., Bouwer and Rice, 1976; Dagan, 1978) appear reasonable for tests performed in wells screened across the water table, when used with the appropriate effective casing radius and normalized head range. The results of this test program indicate that multiple slug tests should always be performed at wells screened across the water table to reliably assess the sufficiency of well development and the appropriateness of conventional theory.
The slug test is a commonly used technique for the in situ estimation of hydraulic conductivity at sites of suspected groundwater contamination (Chirlin, 1990; Butler et al., 1996; Butler, 1996). This approach consists of measuring the recovery of head in a well after a near instantaneous change in water level at that well. The recovery data can be used to estimate the hydraulic conductivity (K) of the formation through comparisons with theoretical models of test responses. The widespread use of this technique cannot be overemphasized, as literally tens of thousands of these tests are performed each year in the United States alone.
A common field application of slug tests is in shallow wells that partially penetrate unconfined flow systems. Many of these wells are screened across the water table in order to detect the presence of low-density contaminants. Common methods for the analysis of slug tests in unconfined formations (Bouwer and Rice, 1976; Dagan, 1978; Amoozegar and Warrick, 1986; Hyder and Butler, 1995) are based on a series of simplifying assumptions concerning the slug-induced flow system. Although the ramifications of the most important of these assumptions have been assessed for wells screened some distance below the water table (e.g., Hyder and Butler, 1995), the appropriateness of these assumptions for wells screened near/across the water table has not yet been fully evaluated. Two related assumptions of particular importance in this setting are: 1) the water table can be represented as a constant-head boundary, and 2) flow above the water table can be ignored. Butler et al. (1994) have performed a limited assessment of these assumptions using a numerical model to simulate slug-induced flow in both the saturated and unsaturated domains. Apparently, however, little work has been done to assess the appropriateness of these assumptions in a field setting.
The purpose of this presentation is to present the findings of a detailed field evaluation of slug tests in wells screened across the water table. A series of slug tests were carried out at three sites in an alluvial aquifer near Lawrence, Kansas, in the summer and fall of 1996. At each site, a test program was designed to assess the appropriateness of the conventional set of assumptions concerning the slug-induced flow system. Consideration of the results from all three sites allows some conclusions to be reached about the viability of standard methods for the analysis of data from slug tests performed in wells screened across the water table.
On the basis of available drill logs and a series of test borings, three sites were chosen in the unconsolidated alluvial aquifer underlying the Kansas River valley near Lawrence, Kansas. The primary criterion for site selection was the existence of an interval of moderate to high hydraulic conductivity (K) extending for some vertical distance on either side of the water table. Since multiple tests were to be performed in each well, sites at which the water table was in material of low K were rejected. At each site, a well was installed by drilling a borehole using conventional hollow-stem augering techniques. Upon reaching the target depth, well screen and casing were inserted through the center of the augers and the flights were pulled back, allowing the formation to collapse against the screen. Sand was then added to bring the filter pack above the top of the screen, a layer of bentonite pellets was placed ontop of the filter pack, and alternating layers of grout and backfill were used to fill the annulus to the surface. At all sites, the top of the filter pack was considerably above the maximum water-table elevation during the period of testing.
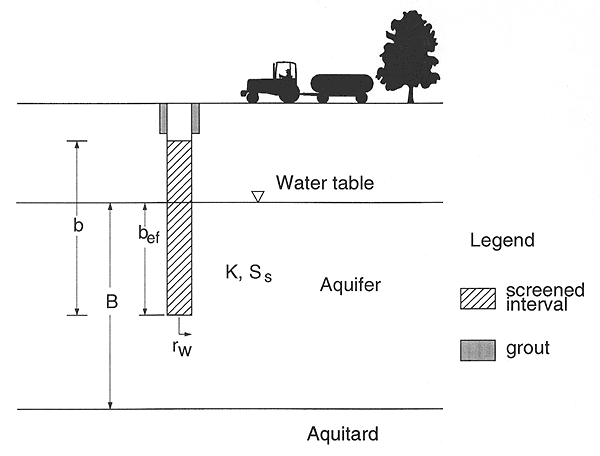
The well-formation configuration for all sites was similar to the schematic cross-section of Figure 1. Table 1 provides specific details for each well. Note that the length of saturated screen (bef) varied from day to day as a result of fluctuations in the water table, so a range of values is given for that quantity. Although the exact distance to the underlying aquitard is not known because the drilling was terminated above the lower boundary of the aquifer, approximate distances are given based on drill logs from nearby wells.
Figure 1--Schematic cross-section of well.

Table 1--Details on each well. rw = nominal radius of well screen; bef = length of saturated well screen; b = total length of well screen; TD = depth to bottom of well screen from top of casing; B = distance from water table to aquitard.
| rw(m) | bef(m) | b(m) | TD(m) | B(m) | |
|---|---|---|---|---|---|
| Collister | 0.051 | 1.51-2.06 | 3.28 | 9.43 | approx. 12.17 |
| Burcham Park | 0.051 | 1.31-2.17 | 2.99 | 6.31 | >10.67 |
| Penny | 0.064 | 1.33-1.41 | 4.29 | 7.87 | approx. 13.31 |
Butler et al. (1996), among others, have stressed that the success of a program of slug tests critically depends on well-development procedures. At all three wells, relatively aggressive development procedures (overpumping and surging) were used in an attempt to remove drilling debris from the near-well portions of the formation. The progress of well development was monitored by periodically performing slug tests at each well. If the response data from tests prior to and after a period of development coincided, then development at that well was deemed sufficient for the purposes of this project.
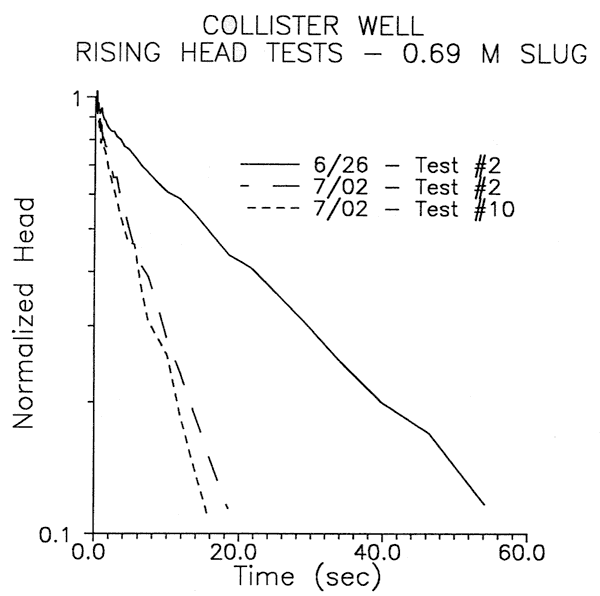
Figure 2 shows the progress of development at the Collister well as monitored by a program of repeat slug tests. Response data are plotted in the format of normalized head (h(t)/Ho, where h is the deviation of head from static conditions and Ho is the size of the initial displacement) versus time since test initiation. The 6/26 test was performed after removing seven well volumes using a 12V purge pump, while the 7/2 tests were performed in the midst of a sequence of overpumping and surging using a high-capacity pump. Note that a near-clear stream of water was produced after development on 6/26, even though the development was actually far from complete. This situation, which has been observed at many other sites as well, indicates that the turbidity of the pumped water is not a reliable indication of the sufficiency of well-development activities for slug tests. The tests reported in the remainder of this presentation were all performed after development at a well had been deemed sufficient as a result of repeat slug tests.
Figure 2--Comparison of three slug tests for Collister well.
The majority of slug tests performed for this project were initiated by rapidly introducing/removing a solid object (slug) to/from the water column. In this case, the slug was a piece of 0.06 m OD PVC pipe, filled with sand, and capped at both ends. Slugs of two different lengths (0.69 m and 1.55 m) were used to assess the dependence of test responses on the magnitude of the initial displacement. A limited number of experiments were also performed using slugs with tapered end caps in an attempt to reduce the disturbance associated with test initiation.
An additional series of tests were performed at each well using a mechanical packer and standpipe (0.05 m ID PVC pipe or 0.10 m ID flexible tubing) arrangement. The mechanical packers, which were mounted on 0.05 m ID pipe, were positioned at or below the water table. A specially designed endpiece attached to the lower end of the packer string allowed the hydraulic connection between the standpipe and the well to be controlled from the surface by moving a piston into/out of the endpiece using pump rods. Falling-head slug tests could be performed by adding water to a closed standpipe and then initiating the test by moving the piston out of the endpiece.
In all cases, recovery data were collected using pressure transducers connected to a PC-based data-acquisition system. Acquisition rates, which ranged from 2-20 Hz, were constant for any given test.
Modeling studies have produced dissimilar conclusions concerning slug tests in wells screened at or near the water table as a result of the use of different assumptions concerning the influence of the unsaturated zone (e.g., Butler et al., 1994; Belitz et al., 1995). In an attempt to clarify this issue, a series of slug tests at each well were directed at assessing the role of the unsaturated zone.
Figure 3 presents the results of tests performed at the Collister well. The results are plotted in the format of normalized head versus normalized time (t/(rc)2, where rc is the effective casing radius). Response data from four tests are presented, three of which were performed in a falling-head (f-h) mode, and one of which was performed in a rising-head (r-h) mode. In the f-h test performed with the solid slug (ss), water could move laterally through the screen and into the unsaturated zone. Such movement was not possible in the standpipe (sp) tests. As shown in Figure 3, the response data from all four tests approximately coincide when plotted using normalized times. This agreement, which was seen in all tests at this well, is an indication that there is little exchange of water between the well and the unsaturated zone. Note that on Figure 3 test responses approximately coincide, even though Ho varied from -0.48 m to 0.57 m, an indication that representing the water table as a fixed boundary is a reasonable approximation for these tests.
Figure 3--Results of four slug tests for Collister well.
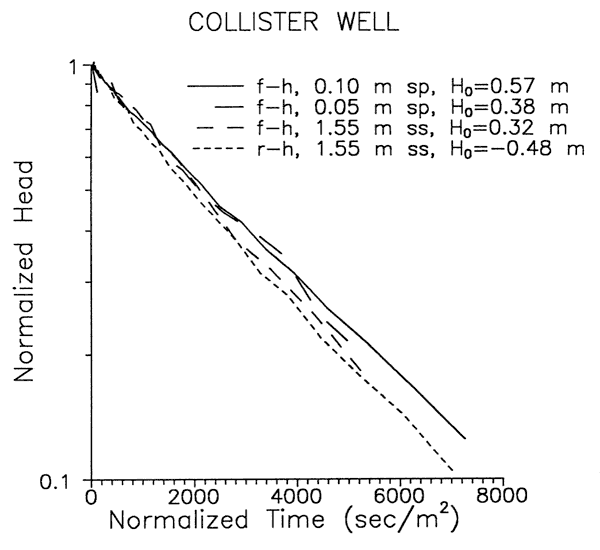
Figure 4 presents the results of a similar series of tests performed at the Penny well. Close agreement is again seen when test data are plotted in a normalized time format. Thus, the role of the unsaturated zone also appears to be of little significance at this site. Note that the tests in Figure 4 appear to be independent of Ho, indicating that the water table can be represented as a fixed boundary during these tests.
Figure 4--Results of three slug tests for Penny well.
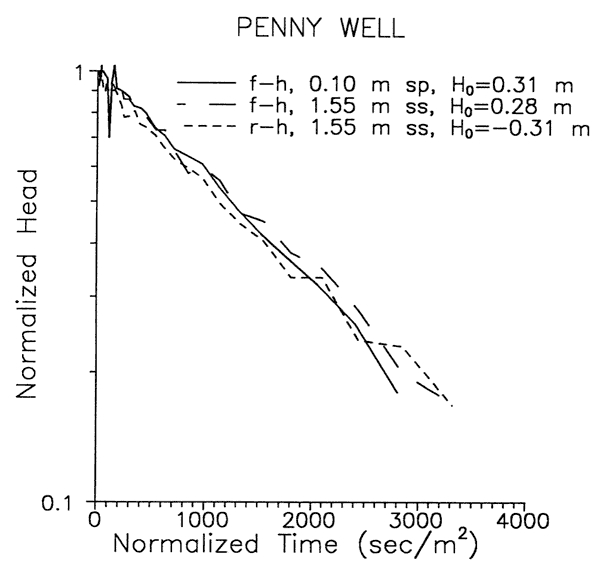
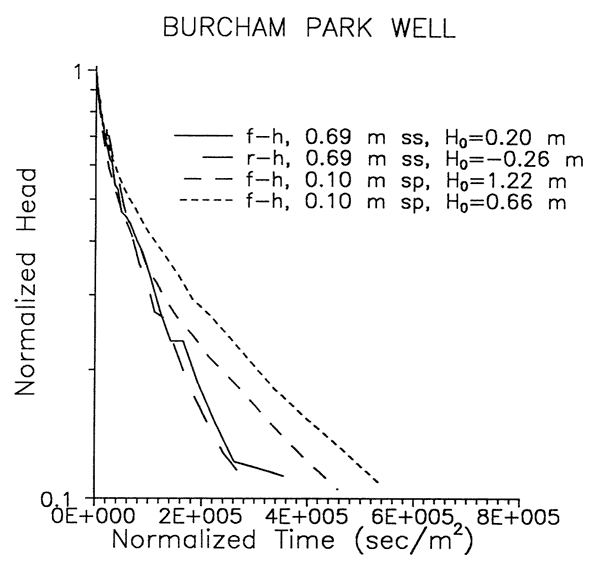
Figure 5 presents the results of a similar series of tests at the Burcham Park well. Although normalized response data from the f-h and r-h solid slug tests approximately coincide, indicating that unsaturated zone effects can be ignored and the water table can be considered a fixed boundary at small Ho, the f-h standpipe tests are not in agreement with the solid slug tests. However, this lack of agreement is primarily a result of packer circumvention and not an indication of significant flow into the unsaturated zone. The packer circumvention, which is essentially just an expression of the double straight line effect of Bouwer (1989), results in the actual effective casing radius of the standpipe tests (nominal standpipe radius used in Figure 5) being the same as the effective radius of the solid slug tests. Although the dependence of the duration of the standpipe tests on Ho could be an indication of a rising water table, it is most likely an artifact of packer circumvention.
Figure 5--Results of four slug tests for Burcham Park well.
The results of these tests indicate that at all three wells the unsaturated zone can be ignored and the water table can be considered a fixed boundary. A comparison of normalized responses from repeat slug tests in which the magnitude of Ho differs is the most effective means of assessing the appropriateness of these assumptions at any given site.
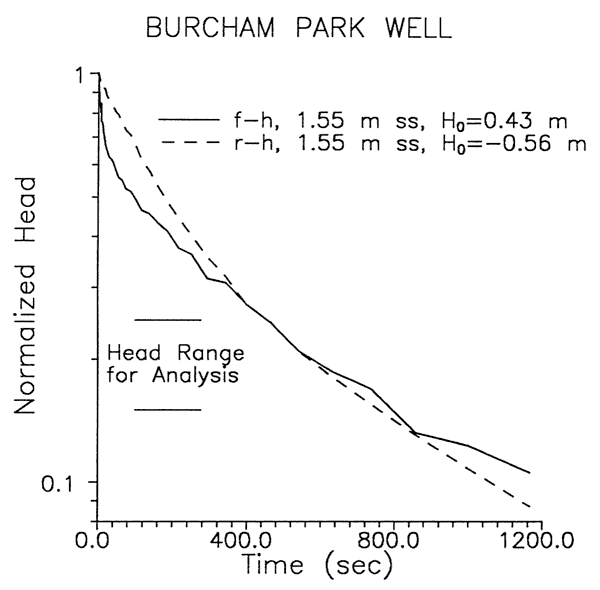
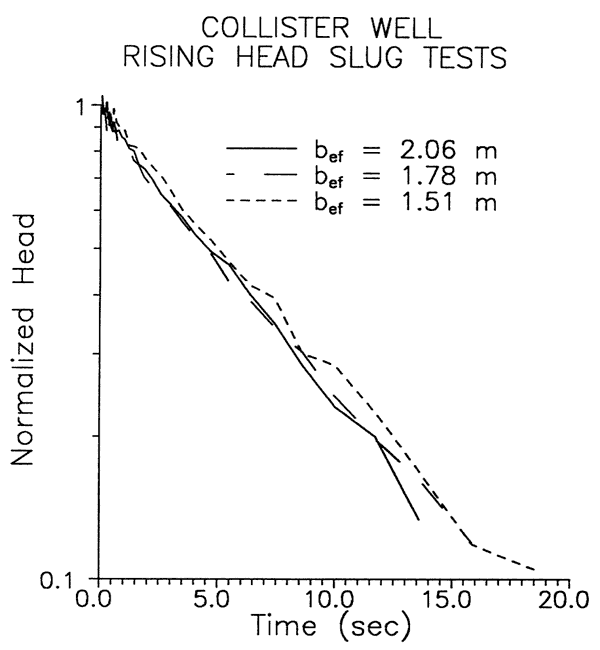
In practice, most slug tests in wells screened across the water table are performed in the rising-head mode in an attempt to diminish the impact of the unsaturated zone on test responses. However, the results described in the previous section indicate that the unsaturated zone had relatively little influence on test responses at the wells examined in this work. The major difference between f-h and r-h tests seen at the Collister and Penny wells was caused by changes in the effective casing radius (rc). Figure 6 displays data from a pair of f-h and r-h tests performed at the Collister well. The effective casing radius for each test can be estimated from a mass balance based on the difference between the expected and actual values for Ho:
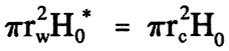
where
Ho* = expected value for the initial displacement;
Ho = actual measured value for the initial displacement.
Figure 6--Comparison of falling-head and rising-head slug tests for Collister well.
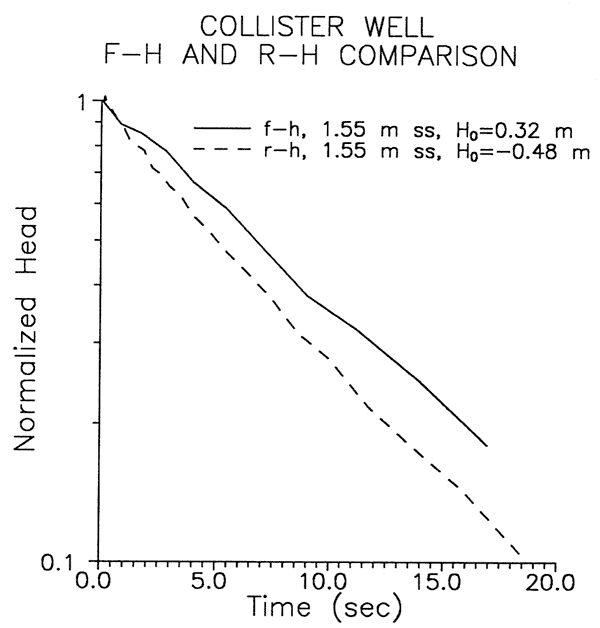
Table 2 lists the Ho* and Ho values for the tests initiated with solid slugs. Note that the site averages of the Ho to Ho* ratio are greater than 83% for r-h tests, an indication that the nominal casing radius (rw) is a reasonable estimate for the effective casing radius in r-h tests. The r-h Ho to Ho* ratios are lower than expected at the Collister and Penny wells as a result of noninstantaneous slug introduction, i.e. the recovery was so rapid at these wells that slug introduction cannot be considered instantaneous with respect to the formation response. The smaller ratios found in the f-h tests are thought to be caused by voids above the water table created during well installation. At both the Collister and Penny wells, data from f-h and r-h tests coincide (see Figures 3 and 4) when the test times are normalized by the effective casing radius calculated from the mass balance, a rather convincing demonstration of the role of the effective casing radius in these tests.
Table 2--Results for tests initiated with solid slugs.
| Collister | Falling Head | Small Slug | Ho approx. 49% of Ho* |
| Large Slug | Ho approx. 37% of Ho* | ||
| Rising Head | Small Slug | Ho approx. 83% of Ho* | |
| Large Slug | Ho approx. 84% of Ho* | ||
| Burcham Park | Falling Head | Small Slug | Ho approx. 82% of Ho* |
| Large Slug | Ho approx. 75% of Ho* | ||
| Rising Head | Small Slug | Ho approx. Ho* | |
| Large Slug | Ho approx. Ho* | ||
| Penny | Falling Head | Small Slug | Ho approx. 83% of Ho* |
| Large Slug | Ho approx. 80% of Ho* | ||
| Rising Head | Small Slug | Ho approx. 92% of Ho* | |
| Large Slug | Ho approx. 87% of Ho* | ||
|
Ho* = theoretical Ho Ho = measured Ho |
|||
| Collister: |
Ho* for the small slug is 0.256 m Ho* for the large slug is 0.561 m |
||
| Burcham Park: |
Ho* for the small slug is 0.256 m Ho* for the large slug is 0.561 m |
||
| Penny: |
Ho* for the small slug is 0.158 m Ho* for the large slug is 0.344 m |
||
Figure 7 shows that the most striking difference between f-h and r-h tests at the Burcham Park well is in the degree of curvature exhibited by the response data when plotted in a log head versus time format. The greater concave-upward curvature seen in the f-h tests is most likely a result of filling partially saturated pore spaces as the water table rises a small amount in the early portions of a test. Although the storage mechanisms differ, this effect is analogous to that seen in slug tests in confined formations with large storage parameters (Chirlin, 1989). Note that if the double straight line approach (Bouwer, 1989) is employed to analyze the test data using the normalized head ranges recommended by Butler (1996), a K estimate equal to that from the r-h tests will be obtained when the effective casing radius calculated from the Ho mass balance is used in the analysis.
Figure 7--Comparison of falling-head and rising-head slug tests for Burcham Park well.
The results of this comparison of rising- and falling-head slug tests indicate that the two types of tests will give very similar results if analyzed in the appropriate fashion. In all cases, a mass balance should be performed to estimate the effective casing radius and test data should be analyzed using the normalized head range recommended by Butler (1996).
Table 1 shows that there were significant fluctuations in the position of the water table during the test period at the Collister and Burcham Park wells. Such fluctuations, which in this case were primarily controlled by stage changes in the nearby Kansas River, can be exploited to gain some insight into the nature of vertical variations in K at a site.
Figure 8 displays data from the Burcham Park well for r-h slug tests performed at four different water-table positions. If the lower 1.31 m of the screen, and the intervals from 1.31-1.51 m, 1.51-1.82 m, and 1.82-2.02 m are designated as layers 1 through 4, respectively, then a rough estimate of the K for each layer can be obtained using the K estimates from each slug test and a thickness-weighted arithmetic average to represent the contribution of individual layers to the slug-test parameter estimate:
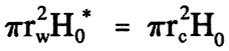
Kst = K estimated from analysis of slug test;
Ki = K of layer i;
bi = thickness of layer i.
Figure 8--Comparison of rising-head slug tests for Burcham Park well at four different water-table positions.
Using the tests shown in Figure 8 and the above equation, K estimates of 0.24 m/d, 1.36 m/d, 1.36 m/d, and 0.054 m/d were obtained for layers 1 through 4, respectively. This result indicates that the zone 1.31-1.82 m above the bottom of the screen (layers 2 and 3) is of much higher conductivity than the material opposite the remainder of the tested interval.
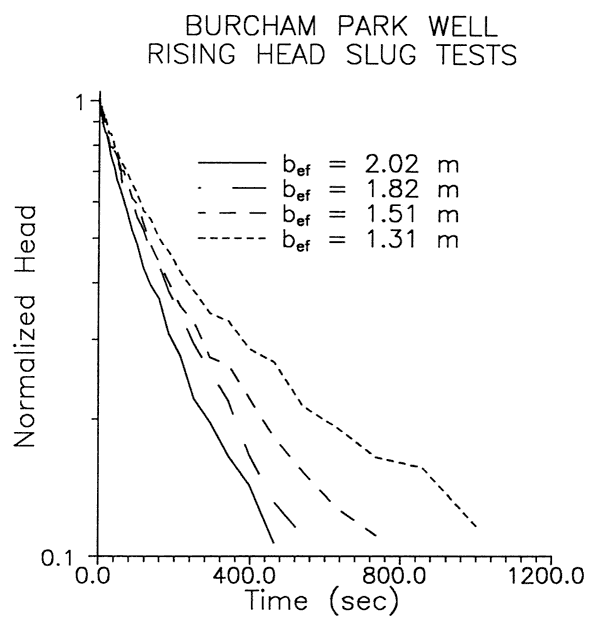
Figure 9 displays data from the Collister well for r-h slug tests performed at three different water-table positions. A similar calculation at this well found that the lower 1.51 m of the well screen had a K value of 23 m/d, while the K of the remainder of the tested interval was essentially negligible in comparison. This finding of a very large vertical difference in K was supported by straddle packer tests performed at the well. Note that the K for the lower 1.51 m is the average value for that interval. Given the degree of vertical variability found at this well, one might expect that the K of the most conductive portion of this interval could be much larger.
Figure 9--Comparison of rising-head slug tests for Collister well at three different water-table positions.
The position of the water table did not change significantly during testing at the Penny well, so little can be said about the vertical variability in K at that well on the basis of available slug test data.
A detailed field evaluation of slug tests in wells screened across the water table was carried out in three wells sited in moderate to high K intervals of a near-surface alluvial aquifer. The major findings of this investigation are as follows:
The major conclusion that can be drawn from the results of this test program is that conventional techniques (e.g., Bouwer and Rice, 1976; Dagan, 1978) appear reasonable for the analysis of response data from slug tests in wells screened across the water table, when used with the appropriate effective casing radius and normalized head range.
Amoozegar, A., and Warrick, A.W., 1986, Hydraulic conductivity of saturated soils: Field methods, in, Methods of Soil Analysis, Part 1, Physical and Mineralogical Methods, edited by A. Klute: Agron. Monogr. Ser. 9, V. 9, pp. 735-770, American Soc. of Agronomy, Madison, Wisc.
Belitz, K., Dripps, W., and Fairchild, J.E., 1995, Slug tests in elastic, unconfined aquifers: Incorporating the free surface: Water Resour. Res., v. 31, no. 12, pp. 3329-3336.
Bouwer, H., 1989, The Bouwer and Rice slug test--An update: Ground Water, v. 27, no. 3, pp. 304-309.
Bouwer, H., and Rice, R. C., 1976, A slug test for determining hydraulic conductivity of unconfined aquifers with completely or partially penetrating wells: Water Resour. Res., v. 12, no. 3, pp. 423-428.
Butler, J.J., Jr., 1996, Slug tests in site characterization: Some practical considerations: Environmental Geosciences, v. 3, no. 3, pp. 154-163.
Butler, J.J., Jr., McElwee, C.D., and Hyder, Z., 1994, Slug tests in unconfined aquifers - Phase two: Kansas Water Resources Research Inst. Contribution No. 310, Manhattan, Ks, 109 pp.
Butler, J.J., Jr., McElwee, C.D., and Liu, W.Z., 1996, Improving the quality of parameter estimates obtained from slug tests: Ground Water, v. 34, no. 3, pp. 480-490.
Chirlin, G.R., 1989, A critique of the Hvorslev method for slug test analysis: The fully penetrating well: Ground Water Monitoring Review, v. 9, no. 2, pp. 130-138.
Chirlin, G. R., 1990, The slug test: The first four decades: Ground Water Management, v. 1, pp. 365-381.
Dagan, G., 1978, A note on packer, slug, and recovery tests in unconfined aquifers: Water Resour. Res., v. 14, no. 5, pp. 929-934.
Hvorslev, M.J., 1951, Time lag and soil permeability in ground-water observations: Bull no. 36., Waterways Exper. Sta., Corps of Engrs., U.S. Army, 50 p.
Hyder, Z., and Butler, J.J., Jr., 1995, Slug tests in unconfined formations: An assessment of the Bouwer and Rice techniques: Ground Water, v. 33, no. 1, pp. 16-22.
We thank the Office of Graduate Studies of the University of Kansas for providing partial travel funding for KLS. Wendy Macpherson of the Department of Geology of the University of Kansas provided assistance in the Collister well tests. JJB is the corresponding author for this report.
Kansas Geological Survey, Geohydrology
Placed online Jan. 5, 2006
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Hydro/Publications/1996/OFR96_46/index.html