Kansas Geological Survey, Open-file Report 1999-8
Next page--Garden City Site
by
James J. Butler, Jr. and John M. Healey
In Support of the
Upper Arkansas River Corridor Study
A Kansas Water Plan Project
KGS Open-file Report 1999-8
Dec. 1999
A series of slug tests were performed by the Kansas Geological Survey in fourteen wells at monitoring sites in Kearny, Finney, and Ford counties in June of 1998 and October of 1999. The major objective of this test program was to acquire estimates of the hydraulic properties of the unconsolidated deposits that serve as the primary aquifers in the area. Hydraulic conductivity estimates obtained from this test program ranged from 2.8-140 ft/day. This range appears quite reasonable for an unconsolidated sequence of interbedded clay- through gravel-sized sediments.
A series of slug tests were performed by the Kansas Geological Survey (KGS) at three monitoring sites in Kearny, Finney, and Ford counties in southwest Kansas in June of 1998 and October of 1999. This work was done as part of the Upper Arkansas River Corridor Study, a multi-year research effort of the KGS directed at determining the fate of saline Arkansas River flows and their effect on aquifer waters in the river valley. Whittemore et al. (1999) provide a brief description of the monitoring sites installed for the project and the information that has been obtained from the sites. This study is a Kansas Water Plan project funded through the Kansas Water Office, Don Whittemore of the Geohydrology Section of the KGS serves as the principal investigator.
The slug tests that are the subject of this report were done to gain better knowledge of the hydraulic properties of the unconsolidated deposits that serve as the primary aquifers in the area. This report describes the procedures used for the performance and analysis of these slug tests. A table summarizing the results of the analyses is presented at the end of the report.
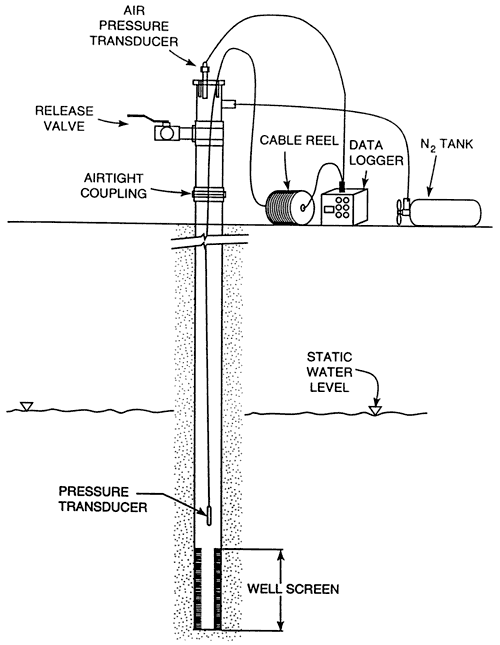
This program of slug tests was carried out following a recently defined set of guidelines for the design, performance and analysis of slug tests (Butler et al., 1996; Butler, 1997). These guidelines were the product of a multi-year KGS research effort directed at improving slug-test methodology. The pneumatic method (Butler, 1997) was used for test initiation at ten of the fourteen monitoring wells. This method involves placing an air-tight wellhead apparatus (Figure 1) on top of the well and pressurizing the air column in the sealed well casing. This pressurization produces a depression of the water level in the well as water is driven out of the well and into the formation in response to the increased pressure in the overlying air column. The water level continues to drop until the magnitude of the total decrease in the pressure head of the water equals the magnitude of the total increase in the pressure head of the air column. At that point, the well has returned to static conditions (i.e. a pressure transducer in the water column has the same reading as prior to pressurization) , and the test can be initiated by a very rapid depressurization of the air column using the release valve shown in Figure 1. A slug test initiated in this manner produces a flow of water into the well. Butler (1997) emphasizes the need to keep the size of the initial water-level change (H0) as small as possible in order to minimize dependence of test responses on H0. The pressure regulation equipment used at the Deerfield and Garden City sites did not allow pressurization at small H0, so some head dependence was observed at wells at those sites. However, better regulation equipment was used at the Dodge City site, so head dependence was essentially negligible at that site.
Figure 1--Hypothetical cross section displaying a well at which the pneumatic method is being used for test initiation (after McLane et al., 1990; Butler, 1997).

Tests were initiated using a solid slug at four of the fourteen wells. The solid slug consisted of PVC pipe, filled with sand and capped at both ends. A hook on the cap at the upper end allowed the slug to be attached to a rope or cable. A slug test can be initiated by introducing the slug into the water column, causing a near-instantaneous rise of water level to begin the test. A slug test can also be initiated by removing the slug from the water column, causing a near-instantaneous drop of water level to begin the test. Prior to the field tests described in this report, an accurate estimate of the water level rise/drop to be expected by introduction/removal of the slug was obtained by calibration in blank casing.
At least four tests were performed at each well following the guidelines of Butler et al. (1996) and Butler (1997). The initial water-level change (H0) was varied by close to a factor of two during the series of tests at each well in order to assess the dependence of test responses on H0. In addition, an attempt was made to perform at least two of the tests using approximately equal H0 to assess the significance of dynamic skin effects. For each test, a relative measure of recovery to static conditions prior to test initiation was calculated. Recovery exceeded 96% in all of the tests described here. Butler (1997) demonstrated that such a small degree of incomplete recovery (less than 4% in all cases) can be ignored for practical applications. For each test, the ratio of the H0 measured immediately after test initiation over the theoretical H0 (H0*) was calculated. This ratio is useful for assessing the relative speed of test initiation (Butler, 1997) and for assessing dynamic pressure effects. The pressure transducers used in this work are designed to measure the static pressure exerted by an overlying column of water. If the acceleration of the water column is great enough, the measurement provided by the pressure transducer is not an accurate reflection of the position of the water level. In that case, the dynamic pressure correction proposed by Brian Zurbuchen of the Univ. of Nebraska at Lincoln (personal communication, 1999) may be necessary. An H0 to H0* ratio less than 0.9 is often an indication that the dynamic pressure correction is necessary.
For all the slug tests described in this report, changes in water level were measured using a pressure transducer (an In-Situ PXD-261 series 0-20 psig transducer) connected to a data logger (Campbell Scientific model CR500 or CR23X). Air pressure within the sealed casing was monitored using a pressure transducer (an InSitu PXD-261 series 0-20 psig transducer) and an analog pressure gauge (Davis Instruments Model 1082 series 0-30 psig gauge). Casing pressurization was accomplished using a gasoline-powered air compressor or nitrogen gas cylinders.
The slug-test response data were analyzed by comparing the data to theoretical models thought to closely resemble the test configuration. In this work, five theoretical models of slug tests in confined and unconfined aquifers were used: 1) the model of Cooper et al. for slug tests in fully penetrating wells in confined aquifers (Cooper et al., 1967; Butler, 1997); 2) the KGS model for slug tests in partially penetrating wells in confined or unconfined aquifers (Hyder et al., 1994; Butler, 1997); 3) the Hvorslev model for slug tests in partially penetrating wells in confined aquifers (Hvorslev, 1951; Butler, 1997); 4) the high-K Hvorslev model (linearized variant of the model of McElwee et al. (Butler, 1997; McElwee and Zenner, 1998)) for slug tests in confined aquifers; and 5) the Bouwer and Rice model for slug tests in partially penetrating wells in unconfined aquifers (Bouwer and Rice, 1976; Butler, 1997).
In all cases, the general strategy for the analysis followed the guidelines presented in Chapter 13 of Butler (1997). Analyses using the Cooper et al., KGS, Hvorslev, and Bouwer and Rice models were performed with Aquiferwin32, an automated well-test analysis package (Environmental Simulations, Inc., 1999), while analyses using the high-K Hvorslev model were performed following an approach described by Butler and Healey (1999). This involved graphical comparisons of data plots with type curves generated using the Mathcad software package (MathSoft, 1997).
The primary parameter of interest for the test program described in this report was hydraulic conductivity (K). A considerable amount of research (e.g., Cooper et al., 1967; McElwee et al., 1995) has shown that single-well slug tests do not provide good estimates of specific storage as a result of the insensitivity of test responses to the storage parameter and uncertainty regarding the effective screen radius. The regular and high-K variants of the Hvorslev model, and the Bouwer and Rice model invoke this insensitivity as justification for the mathematically convenient neglect of the influence of specific storage on slug-test responses. Thus, the effect of specific storage was assumed negligible for analyses performed with these models. Estimates of specific storage obtained with the Cooper et al. and KGS models were used as screening tools following the guidelines outlined in Chapter 13 of Butler (1997).
In general, one should not expect slug tests to produce hydraulic conductivity estimates that are equal to those obtained from the analysis of pumping-test data. As emphasized by Butler (1997), the effect of incomplete well development on parameter estimates determined from slug tests will be difficult to avoid, so K estimates obtained from slug tests should always be considered as lower bounds on the hydraulic conductivity of the formation in the vicinity of the test interval. The existence of an anisotropy in hydraulic conductivity can lead to a further under-prediction, since the assumption of isotropy is commonly adopted for analysis purposes. Incomplete development and anisotropy, however, will have much less of an impact on parameters determined from analyses of drawdown measured during a pumping test. Thus, hydraulic conductivity estimates determined from pumping tests are generally larger than those determined from slug tests (Butler and Healey, 1998).
In order to compare values from different sites, hydraulic conductivity estimates are usually converted to the standard laboratory conditions for reporting hydraulic conductivity values (pure water at 15.6 deg. C (Fetter, 1994)). Temperature data collected in June of 1998 (Deerfield and Garden City sites) and in March of 1999 (Dodge City site) indicated that the maximum difference from standard laboratory conditions was 2.5 deg. C, so the temperature correction was not necessary (less than 7% correction in worst case). Although total dissolved solids measurements approached 3000 mg/l, laboratory data detailing viscosity and density changes as a function of sodium chloride concentration (Weast, 1976) indicate that the hydraulic conductivity estimates do not need to be corrected for salinity at any of the wells discussed in this report (less than 0.2% correction in worst case).
In the following sections, the results of the analyses of the tests performed at each monitoring site will be described in the order in which the tests were performed.
The Deerfield site is located in Kearny County on the grounds of Deerfield High School (Figure 2). The site consists of five wells screened over different vertical intervals in the alluvial and underlying High Plains aquifers. Table 1 provides well construction information for the site, while Table 2 provides the schedule and details of the slug tests performed at the site.
Figure 2--Location map for Deerfield monitoring site.
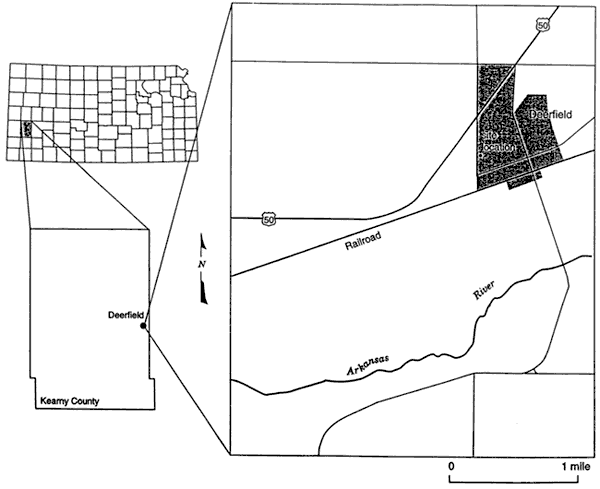
Table 1--Well construction information for wells at Deerfield monitoring site.
| Well No. | Borehole Radius (ft) |
Casing Radius (ESR)1 (ft) |
Total Depth2 (ft) |
NSI3 (ft) |
Grout Interval4 (ft) |
|---|---|---|---|---|---|
| DOW-1 | 0.250 | 0.103 (0.250) | 3385 | 326-336 | 0-316 |
| DOW-2 | 0.250 | 0.103 (0.250) | 249 | 239-249 | 0-234 |
| DOW-3 | 0.250 | 0.103 (0.250) | 144 | 134-144 | 0-123 |
| DOW-4 | 0.312 | 0.168 (0.312) | 68 | 60-68 | 0-48 |
| DOW-5 | 0.312 | 0.168 (0.312) | 46 | 36-46 | 0-35 |
| 1--ESR or effective screen radius. In high-K formations, the effective screen radius may be closer to the nominal radius of the well screen (Butler, 1996). 2--depths are from top of casing in this and remaining columns 3--NSI = nominal screened interval 4--neat cement grout 5--depth includes a sump at bottom of screen |
|||||
Table 2--Schedule and details of slug tests performed at the Deerfield monitoring site
| Date | Test Well 1 |
Test No. |
H0* (ft) 2 |
%Rec 3 | H0/H0* 4 |
|---|---|---|---|---|---|
| 6/17/98 | DOW-1 | 1 | 3.84 | 100.0 | 1.08 |
| 2 | 8.68 | 99.9 | 1.04 | ||
| 3 | 8.50 | 99.7 | 1.06 | ||
| 4 | 3.56 | 99.5 | 1.03 | ||
| 6/17/98 | DOW-2 | 1 5 | 4.14 | 99.9 | 0.99 |
| 2 | 8.96 | 100.0 | 1.01 | ||
| 3 6 | 8.65 | 99.9 | 0.98 | ||
| 4 6 | 4.12 | 99.9 | 0.97 | ||
| 6/17/98 | DOW-3 | 1 | 4.41 | 99.5 | 0.96 |
| 2 | 8.73 | 99.4 | 0.91 | ||
| 3 | 8.92 | 99.4 | 0.93 | ||
| 4 | 4.28 | 99.5 | 0.87 | ||
| 6/17/98 | DOW-4 7 | 1 | 0.84 | 99.2 | 0.69 |
| 2 | 0.84 | 99.3 | 0.98 | ||
| 3 | 1.84 | 99.1 | 0.87 | ||
| 4 | 1.84 | 99.8 | 0.95 | ||
| 5 | 0.84 | 98.0 | 0.74 | ||
| 6/17/98 | DOW-5 7 | 1 | 0.84 | 98.8 | 0.63 |
| 2 | 0.84 | 98.2 | 0.82 | ||
| 3 | 1.84 | 99.1 | 0.57 | ||
| 4 | 1.84 | 99.5 | 0.88 | ||
| 5 | 0.84 | 98.3 | 0.49 | ||
|
1--wells listed in order in which tests were performed, tests at wells DOW 1-3 were initiated with the pneumatic method, while tests at wells DOW4-5 were initiated with solid slugs 2--expected H0 measured by air-pressure transducer or calculated from water displaced by solid slug in blank casing 3--percent recovery--relative measure of how close well had returned to static conditions prior to test initiation--one minus ratio of distance from static at time of test initiation over H0 (both based on water-pressure transducer readings) times 100 4--H0 measured at time of test initiation with water-pressure transducer over H0*--values greater than approximately 1.05 are a product of sensor noise and the methodology used to estimate H0 from the water-pressure transducer readings, while values less than about 0.95 may be an indication of a test initiation that was non-instantaneous relative to the formation response or water-pressure transducer readings that need to be adjusted for dynamic pressure effects 5--test inadvertently not run to completion 6--small air leak somewhere in well and well-head apparatus affected H0 reading 7--solid-slug initiation method and high winds caused high noise level making it difficult to obtain reliable estimates of H0/H0* |
|||||
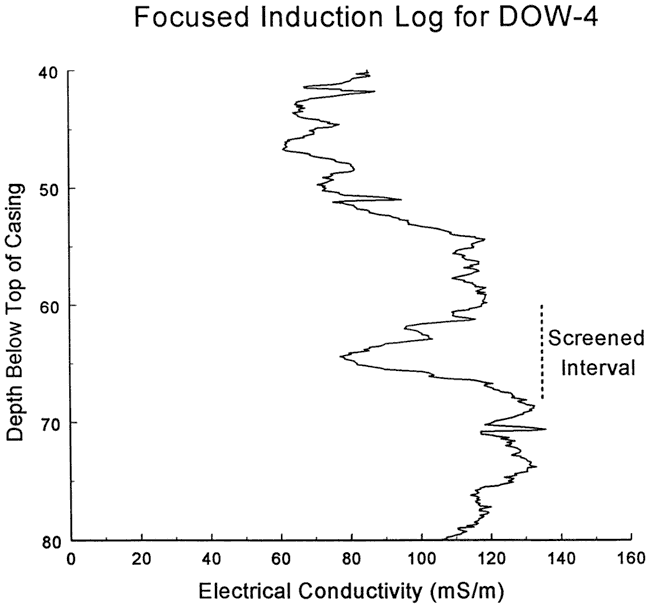
Four slug tests were performed at well DOW-1 on June 17, 1998. Figure 3 is a plot of normalized head versus logarithm of time for this series of tests. As shown in the figure, a small amount of head dependence was observed, which was assumed negligible for analysis purposes. There was no evidence of dynamic skin effects for any of these tests. Test four was selected for analysis because it was slightly faster than tests two and three and had a better H0/H0* ratio than test one. Figure 4 displays the focused induction log in the vicinity of the test interval (no logging data available below screened interval).
Figure 3--Normalized head (H(t)/H0) versus the logarithm of time since test initiation for series of slug tests performed at well DOW-1.
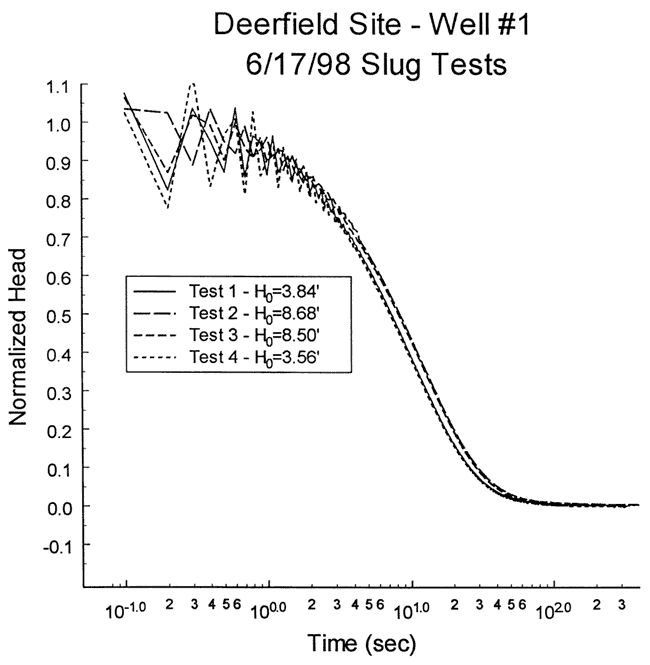
Figure 4--Focused induction log at well DOW-1 for portions of the formation in the vicinity of the screened interval (spike at top of screened interval produced by casing centralizer).
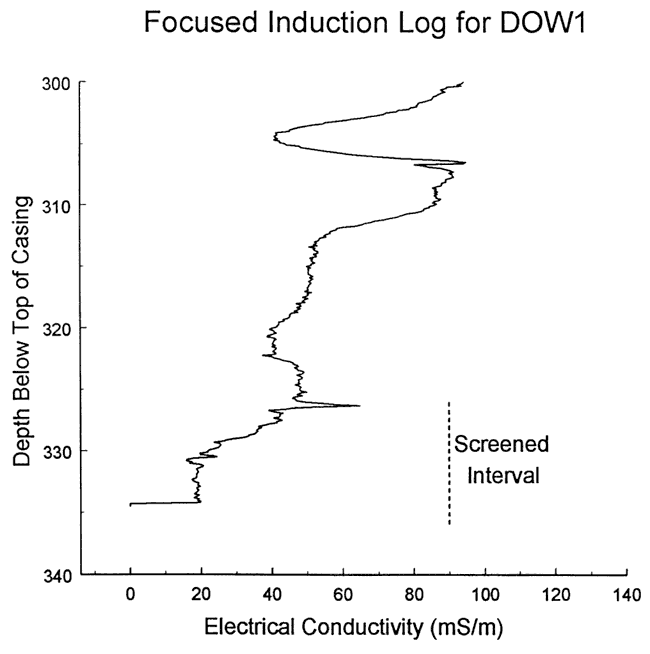
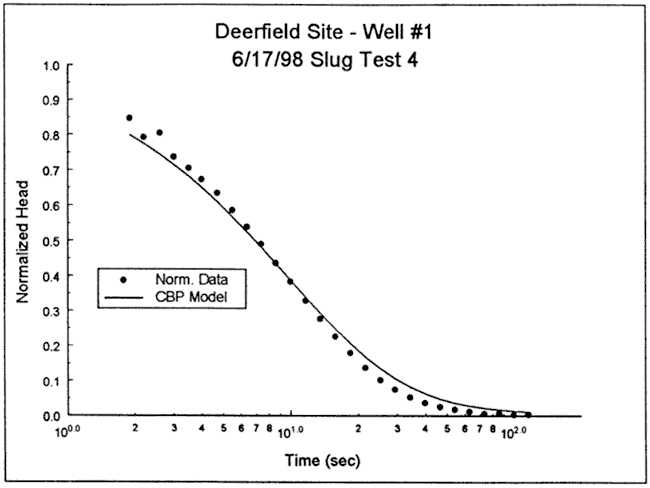
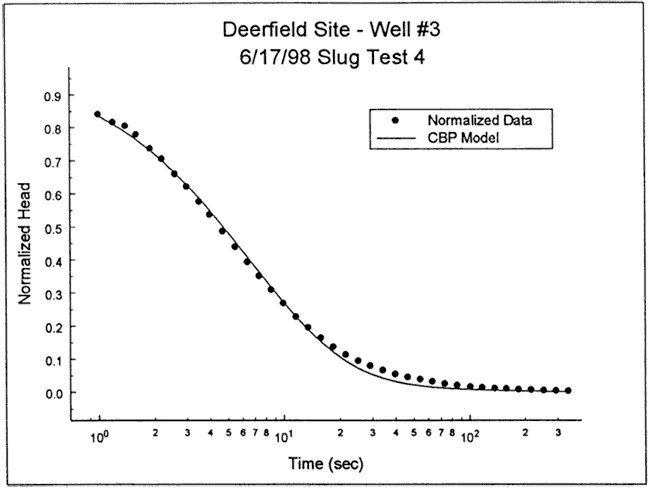
The response data were first analyzed with the fully penetrating well model of Cooper et al. Figure 5 is plot of the normalized data and the best-fit Cooper et al. type curve for a specific storage value at the lower end of the range of physical plausibility (Ss equals 1.7x10-6 ft-1) In this case, a reasonable match could not be obtained with the Cooper et al. model. Given the log of Figure 4 (no apparent barrier to flow immediately above screen), a significant component of vertical flow above the screened interval was considered the most likely explanation for the deviation between the theoretical type curve and field data.
Figure 5--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-1 and the best-fit Cooper et al. type curve.
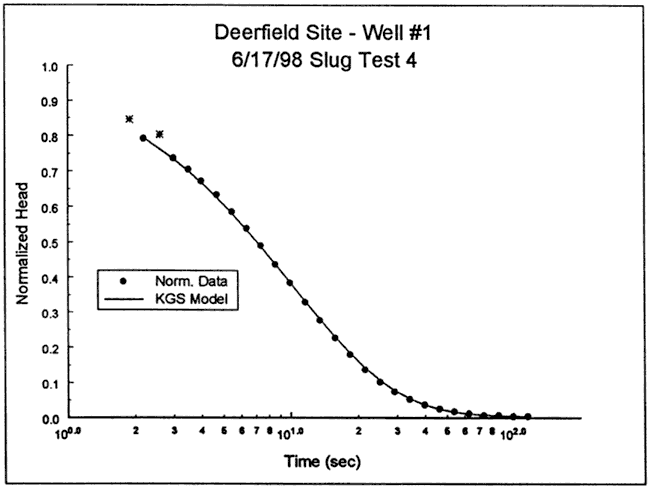
The response data were next analyzed with the KGS model for partially penetrating wells. Because of the noise and the head dependence observed in the test data, specific storage was assumed fixed (Ss=1.7x10-6 ft-1). Figure 6 is a plot of the normalized data and the best-fit KGS model type curve (K=15 ft/day, layer thickness=40 ft; impermeable unit 17 ft above top of screen). Note that the starred points were not considered in the analysis.
Figure 6--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-1 and the best-fit KGS model type curve.
Four slug tests were performed at well DOW-2 on June 17, 1998. Figure 7 is a plot of normalized head versus logarithm of time for this series of tests. As shown in the figure, a small amount of head dependence was observed, which was assumed negligible for analysis purposes. There was no evidence of dynamic skin effects for any of these tests. Test one was selected for analysis because it was slightly faster than tests two and three (test four would have been an equally viable choice). Figure 8 displays the focused induction log in the vicinity of the test interval.
Figure 7--Normalized head (H(t)/H0) versus the logarithm of time since test initiation for series of slug tests performed at well DOW-2.
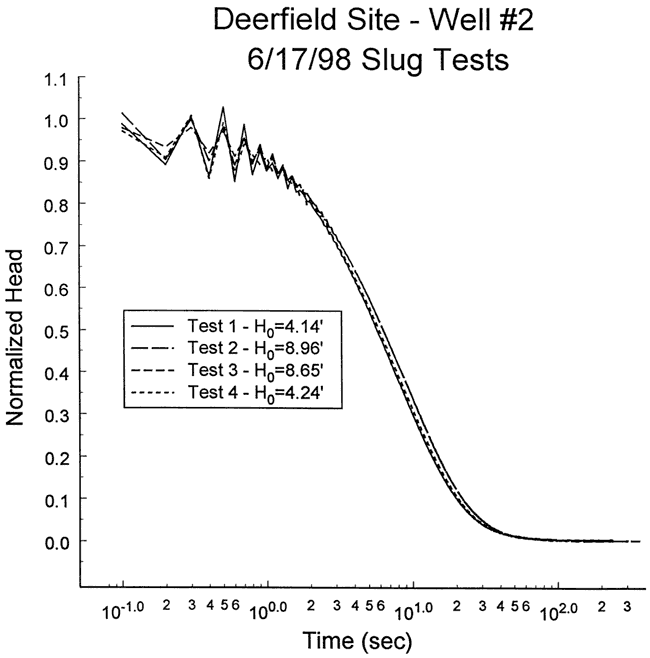
Figure 8--Focused induction log at well DOW-1 for portions of the formation in the vicinity of the screened interval at DOW-2.
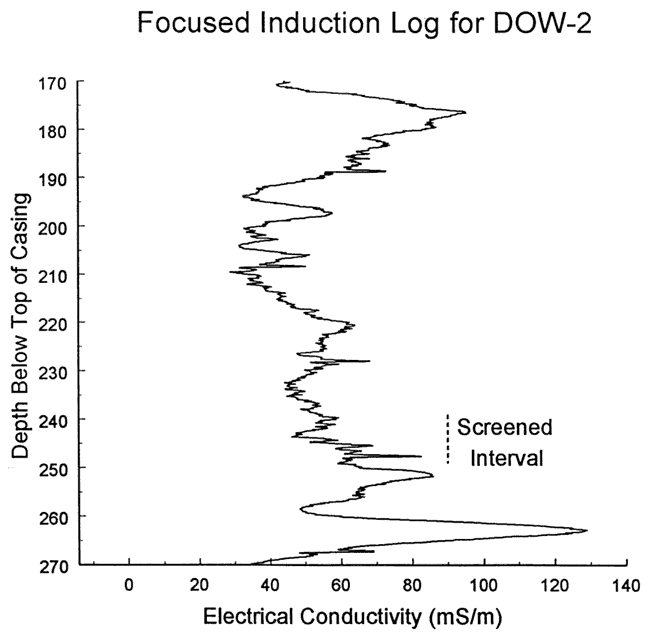
The response data were first analyzed with the fully penetrating well model of Cooper et al. Figure 9 is a plot of the normalized data and the best-fit Cooper et al. type curve for a specific storage value at the lower end of the range of physical plausibility (Ss equals 1.7x10-6 ft-1) In this case, a reasonable match could not be obtained with the Cooper et al. model. Given the log of Figure 8, a significant component of vertical flow was considered the most likely explanation for the deviation between the theoretical type curve and field data.
Figure 9--Normalized head (H(t)/H0) versus log time plot for test 1 at DOW-2 and the best-fit Cooper et al. type curve.
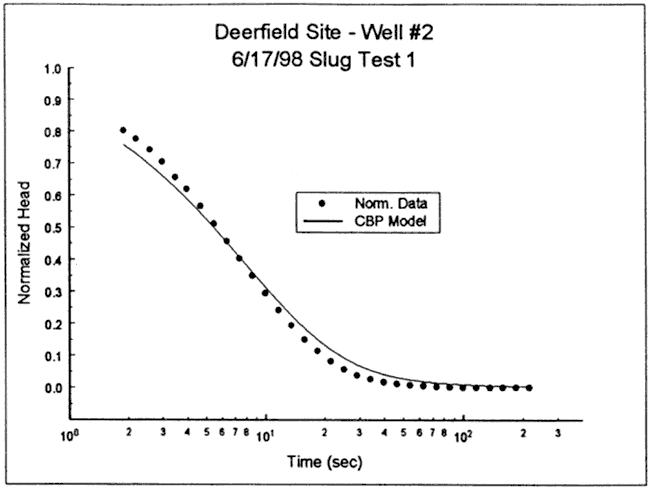
The response data were next analyzed with the KGS model for partially penetrating wells. Because of the noise and the head dependence observed in the test data, specific storage was assumed fixed for the analysis (Ss=1.7x10-6 ft-1) . Figure 10 is a plot of the normalized data and the best-fit KGS model type curve (K=18.3 ft/day, layer thickness=84 ft, impermeable unit 51 ft above top of screen). The deviation observed at early times is assumed to primarily be a product of the slight head dependence displayed in Figure 7. If 0.3 seconds is subtracted from the time of each measurement, an excellent match is obtained. Although there is no justification for such an adjustment, it does confirm that the differences observed on Figure 10 are a product of processes affecting early time data. As a check, these data were also analyzed with the Hvorslev model, resulting in a K estimate within 13% of that obtained with the KGS model.
Figure 10--Normalized head (H(t)/H0) versus log time plot for test 1 at DOW-2 and the best-fit KGS model type curve.
Four slug tests were performed at well DOW-3 on June 17, 1998. Figure 11 is a plot of normalized head versus logarithm of time for this series of tests. As shown in the figure, a very small amount of head dependence was observed, which was assumed negligible for analysis purposes. There was no evidence of dynamic skin effects for any of these tests. Test four was selected for analysis because it displayed slightly less noise than test one, and was slightly faster than tests two and three. Figure 12 presents the focused induction log in the vicinity of the test interval.
Figure 11--Normalized head (H(t)/H0) versus the logarithm of time since test initiation for series of slug tests performed at well DOW-3.
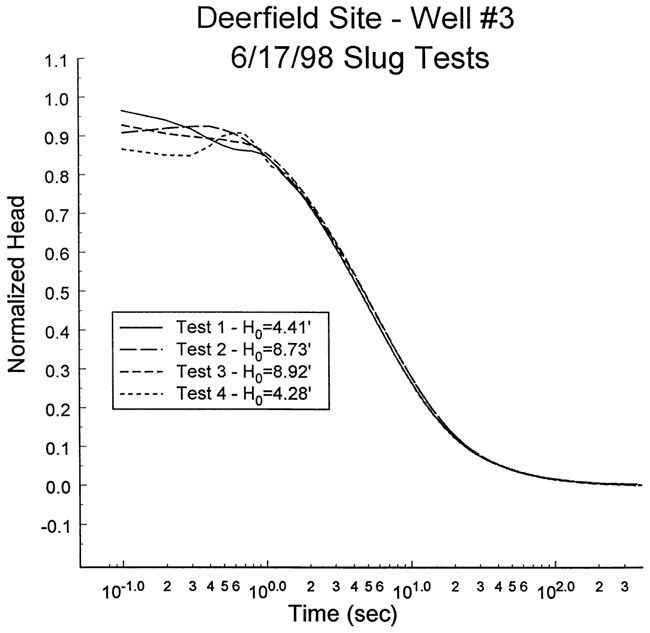
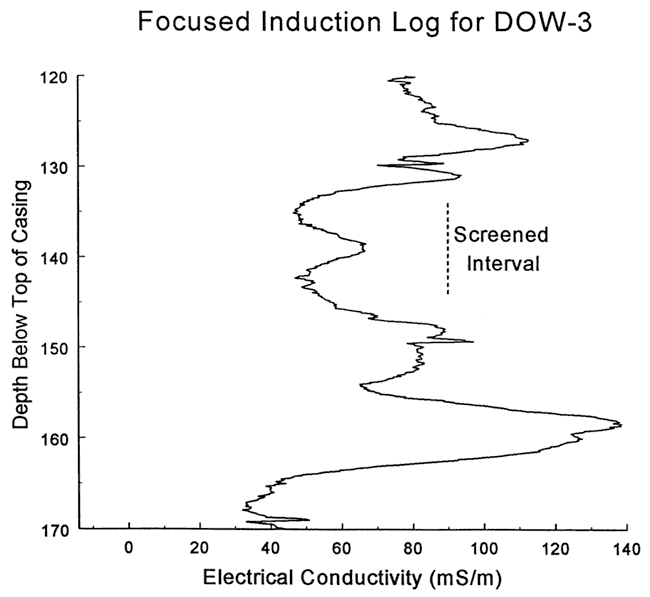
Figure 12--Focused induction log at well DOW-1 for portions of the formation in the vicinity of the screened interval at DOW-3.
The response data were first analyzed with the fully penetrating well model of Cooper et al. Figure 13 is a plot of the normalized data and the best-fit Cooper et al. type curve for a specific storage value at the lower end of the range of physical plausibility (Ss equals 1.7x10-6 ft-1). In this case, a reasonable match could not be obtained with the Cooper et al. model. As shown in the figure, the test data deviated from the theoretical type curve at large times. This deviation, which could not be removed using any value of specific storage, may be a product of lenses of high-K material pinching out at some distance from the test well. It may also be a product of a test in a partially penetrating well in which impermeable boundaries above and/or below the screened interval affect the response data. In addition to the obvious late-time deviation, there is a more subtle systematic deviation for times less than ten seconds. This systematic deviation, which could not be removed using a physically plausible value for specific storage, may be a product of a low-conductivity well skin or a significant component of vertical flow.
Figure 13--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-3 and the best-fit Cooper et al. type curve.
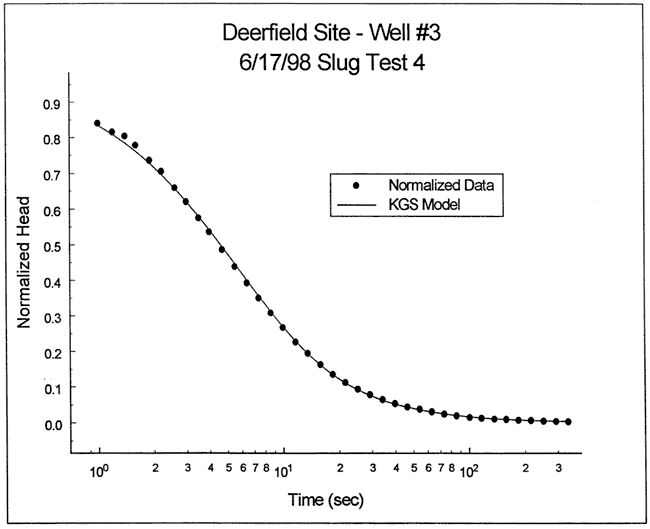
The focused induction log of Figure 12 shows that a zone of relatively low electrical conductivity (assumed relatively high K) extends close to twenty feet in the vicinity of the test interval, so the test data were analyzed with the KGS model for partially penetrating wells (layer thickness=20 ft, impermeable unit 3 ft above top of screen). As with the Cooper et al. analysis, a systematic deviation was observed at late time. Figure 14 is a plot of normalized response data versus a theoretical type curve, clearly displaying a late-time deviation. In this case, a very good fit could be obtained for normalized heads greater than 0.4. In order to fit the data at smaller normalized heads, a two-zone variant of the KGS model was applied (Hyder et al., 1994). This variant enables the effect of high-K lenses pinching out at a distance from the well to be incorporated into the analysis. Figure 15 is a plot of normalized response data versus the best-fit theoretical type curve for the case of an inner zone (31.9 ft in diameter) of higher conductivity than the more distant portions of the formation. The properties of the higher-K inner zone (K=23 ft/day and Ss=8.1x10-6 ft-1) were derived from the analysis of Figure 14, while the properties of the more distant portions of the formation (K=8.7 ft/day and Ss=3.5x10-6 ft-1) were determined using the two-zone variant of the KGS model. Since a comparison of geophysical and drillers' logs from the other wells at this site indicates that zones of sand and gravel do pinch out between wells at this depth, the results from the two-zone model are considered to be reasonable representations of conditions in the test interval.
Figure 14--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-3 and the best-fit KGS model type curve.
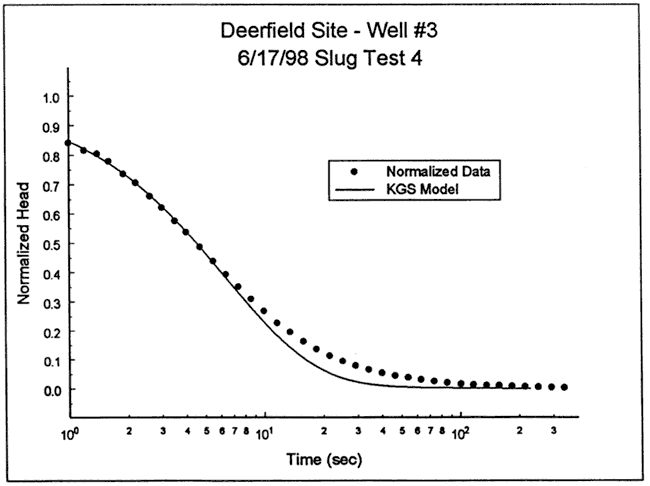
Figure 15--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-3 and the best-fit KGS model (two-zone variant) type curve.
Five slug tests were performed at well DOW-4 on June 17, 1998. Figure 16 is a plot of normalized head versus logarithm of time for this series of tests. The solid slug initiation method coupled with very windy conditions (a wind advisory was in effect during these tests) introduced a great deal of noise into the test data. Although test two appears more rapid than the other tests, this difference is interpreted to be primarily a product of uncertainty regarding H0 and the time of test initiation. Since the other four tests basically coincided, nonlinear mechanisms and dynamic skin effects were assumed negligible. Test four was selected for analysis because the larger H0 for that test produced a lower degree of noise in the normalized data. Figure 17 displays the focused induction log in the vicinity of the test interval.
Figure 16--Normalized head (H(t)/H0) versus the logarithm of time since test initiation for series of slug tests performed at well DOW-4.
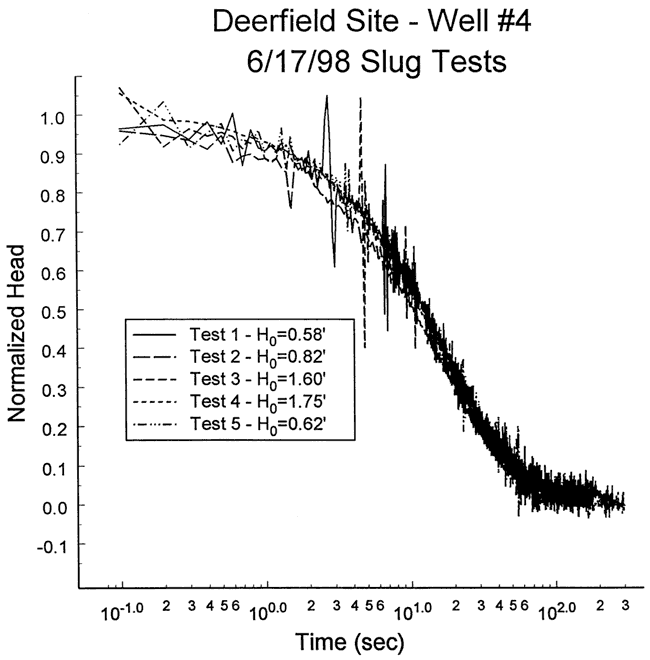
Figure 17--Focused induction log at well DOW-1 for portions of the formation in the vicinity of the screened interval at DOW-4.
The response data were analyzed with the fully penetrating well model of Cooper et al. Figures 18 and 19 are plots of the normalized data and the best-fit Cooper et al. type curve for two different specific storage values (Ss equals 3.3x10-6 ft-1 and 1.4x10-8 ft-1, respectively) . In this case, a reasonable match (K=72 ft/day) could only be obtained using a physically implausible value of specific storage (1.4x10-8 ft-1) . The failure to obtain an acceptable match within the range of physically plausible values of specific storage could be a product of a low-conductivity well skin or a significant component of vertical flow. However, as shown by the focused induction log of Figure 17, there is little reason to invoke a significant component of vertical flow as an explanation for the deviation observed in Figure 18 because the test interval appears to be bounded on both sides by intervals of appreciably higher electrical conductivity (assumed appreciably lower hydraulic conductivity). Thus, the most likely explanation for the deviation is the existence of a low-conductivity well skin. The deviation in Figure 18 is not great, indicating that the hypothesized low-K skin does not have properties dramatically different from those of the layers opposite the test interval.
Figure 18--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-4 and the best-fit Cooper et al. type curve (Ss equals 3.3x10-6 ft-1).
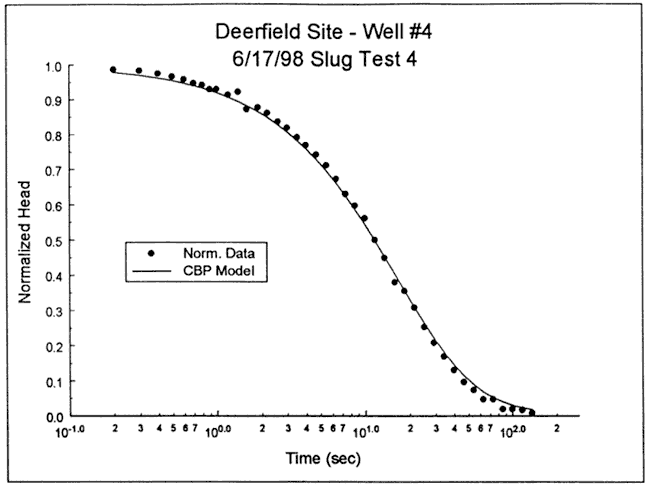
Figure 19--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-4 and the best-fit Cooper et al. type curve (Ss equals 1.4x10-8 ft-1).
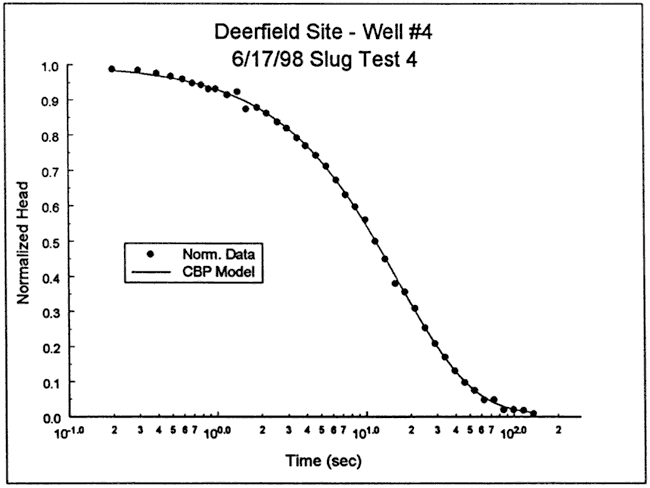
Butler (1997) explains how to interpret hydraulic conductivity estimates obtained in the presence of a low-K skin. For the analysis displayed in Figure 19, there is relatively little uncertainty about the apparent specific storage estimate because the fit degrades markedly with increases or decreases in specific storage. Thus, the hydraulic conductivity estimate of 72 ft/day appears to be a reasonable value for the average hydraulic conductivity of the test interval. Note that an equally good fit can be obtained using the partially penetrating KGS model and a layer thickness of 20 ft (K = 33 ft/day). However, the focused induction log of Figure 17 shows little reason to expect that a partially penetrating model would be appropriate at this well.
Five slug tests were performed at well DOW-5 on June 17, 1998. Figure 20 is a plot of normalized head versus logarithm of time for this series of tests. The solid slug initiation method coupled with very windy conditions (a wind advisory was in effect during these tests) introduced a great deal of noise into the test data. There was a considerable difference between the plots from the various tests. This difference, however, is interpreted to be primarily a product of uncertainty regarding H0 and the time of test initiation, so nonlinear mechanisms and dynamic skin effects were assumed negligible. Test four was selected for analysis because the larger H0 produced a lower degree of noise in the normalized data and the H0/H0* ratio was the closest to one. Figure 21 displays the focused induction log in the vicinity of the test interval.
Figure 20--Normalized head (H(t)/H0) versus the logarithm of time since test initiation for series of slug tests performed at well DOW-5.
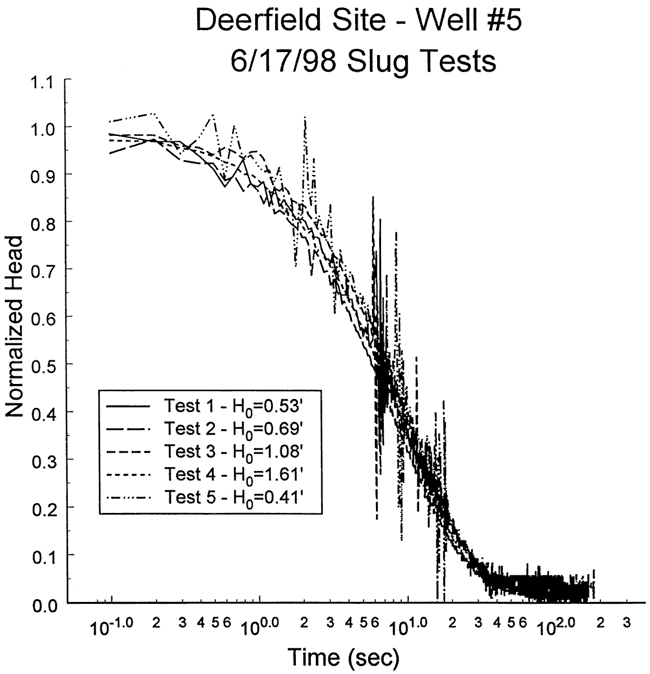
Figure 21--Focused induction log at well DOW-1 for portions of the formation in the vicinity of the screened interval at DOW-5.
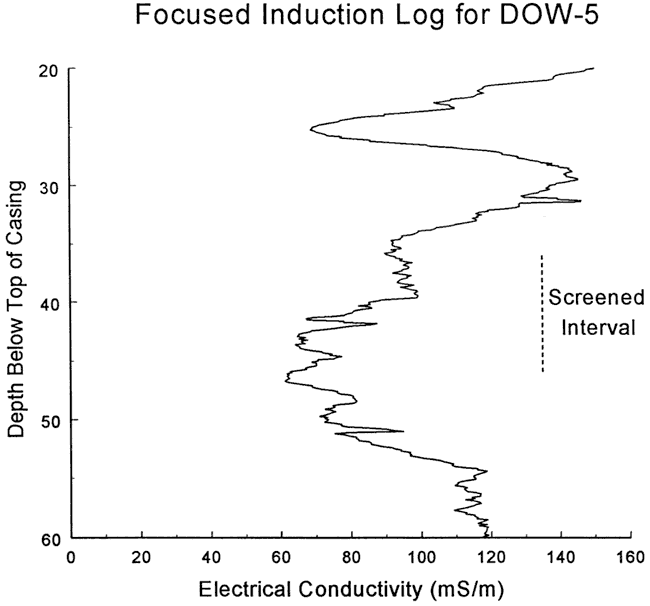
The response data were analyzed with the fully penetrating well model of Cooper et al. Figures 22 and 23 are plots of the normalized data and the best-fit Cooper et al. type curve for two specific storage values (Ss = 2.9x10-6 ft-1 and 1.4x10-10 ft-1. respectively). As shown in the figures, a reasonable match could only be obtained using a physically implausible value of specific storage (1.4x10-10 ft-1) . The failure to obtain an acceptable match within the range of physically plausibility could be the result of a low-K well skin or a significant component of vertical flow. The log of Figure 21 shows that the test interval is bounded by materials of higher electrical conductivity (assumed lower K). Thus, a low-K skin appears to be the most probable explanation.
Figure 22--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-5 and the best-fit Cooper et al. type curve (Ss equals 2.9x10-6 ft-1).
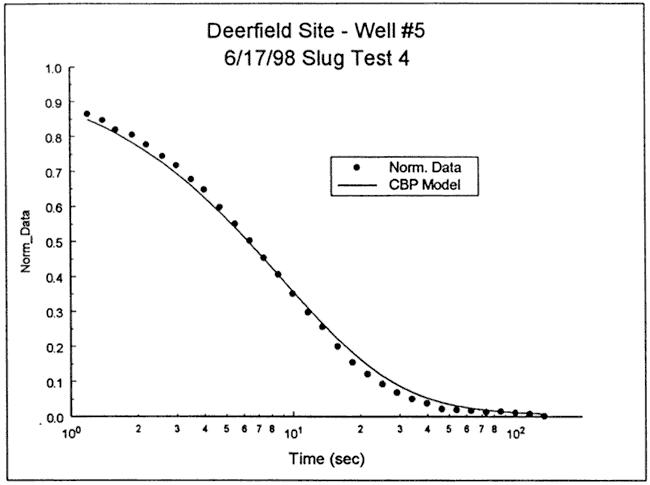
Figure 23--Normalized head (H(t)/H0) versus log time plot for test 4 at DOW-5 and the best-fit Cooper et al. type curve (Ss equals 1.4x10-10 ft-1).
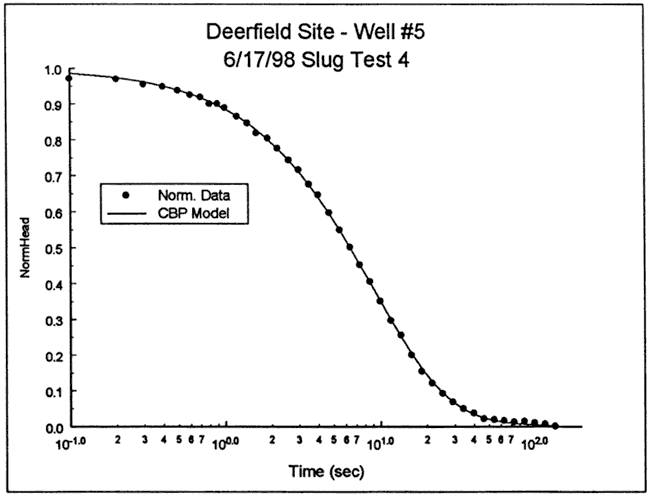
As discussed by Butler (1997), there can be a considerable degree of uncertainty about hydraulic conductivity estimates obtained from slug tests performed in the presence of a low-K well skin. This uncertainty is a result of the nonuniqueness of the type curve fits, i.e. a similarly good fit can be obtained using a wide range of specific storage values. For well DOW-5, this nonuniqueness in the type curve fits translates into a K range of approximately 131-147 ft/day. Note that an equally good fit can be obtained using the partially penetrating KGS model and a layer thickness of 28 ft (K = 47 ft/day). However, the focused induction log of Figure 21 shows little reason to expect that a partially penetrating model with a thickness of 28 ft would be appropriate.
In this report, variations in electrical conductivity (e.c.) are assumed to be reflective of variations in lithology (zones of higher e.c. are assumed to have greater proportions of clay), and thus reflective of variations in K. However, the specific conductance of the water can also be an important determinant of e.c. This is illustrated by the focused induction logs of DOW-1 and DOW-5 (Figures 4 and 21, respectively). The K from DOW-5 is almost an order of magnitude greater than that from DOW-1, but the e.c. values from DOW-5 are considerably higher. The elevated e.c. values at DOW-5 are a result of the specific conductance of the groundwater at DOW-5 being much greater than that at DOW-1. Thus, consideration of groundwater chemistry is necessary when interpreting e.c. variations.
Next page--Garden City Site
Kansas Geological Survey, Geohydrology
Placed online Dec. 6, 2007; original report dated Dec. 1999
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Hydro/Publications/1999/OFR99_08/index.html