Kansas Geological Survey, Open-file Report 1999-16
by
James J. Butler, Jr., and Ming-Shu Tsou,
Kansas Geological Survey, and
Vitaly A. Zlotnik and Huihua Huang
University of Nebraska, Lincoln
Prepared for Presentation at
Spring AGU Meeting, Boston, MA
June 3, 1999
KGS Open-file Report 1999-16
Commonly used methods for estimation of pumping-induced water transfers between streams and aquifers are based on a series of idealistic assumptions about the stream-aquifer interface. Unfortunately, in many cases, these assumptions are not consistent with field conditions. In order to assess the ramifications of some of these assumptions, a new semianalytical solution has been developed for estimation of the drawdown and stream depletion produced by pumping from a well in the vicinity of a stream. This solution, which incorporates a more realistic representation of the stream-aquifer interface, is based on the Dupuit assumptions and a model of incompressible flow across the streambed. The solution will be used to assess the impact of finite stream width, shallow stream penetration, a low-permeability streambed, and a finite-width aquifer on pumping-induced drawdown and stream depletion estimates. Particular attention will be paid to the errors that may be introduced through application of the commonly used approaches (e.g., Jenkins, 1968). The solution will also be compared to recently proposed expressions for the drawdown and stream depletion produced by pumping in the vicinity of an infinitely thin stream (Hunt, 1999). Finally, the solution will be used to help clarify where field efforts should be concentrated in order to improve the reliability of estimates of pumping-induced water transfers.
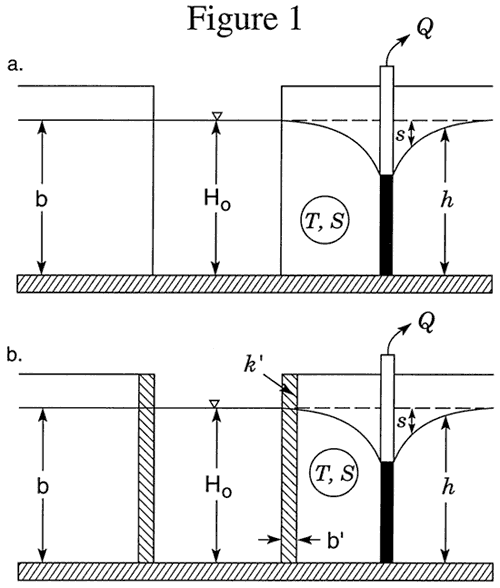
Stream-aquifer interactions can be a key component of the hydrologic budgets of aquifers and streams. Over the last 50 years, several models have been proposed for the estimation of the influence of nearby streams on groundwater development. Theis (1941) was the first to propose a transient model for evaluation of the impact of a stream on pumping activities. This approach, later generalized by Glover and Balmer (1954), is based on a series of idealistic assumptions that include a fully penetrating stream and a perfect hydraulic connection between the stream and the adjoining aquifer (Figure 1a). The Jenkins (1968) implementation of this approach has become a standard tool for use in water-management design and water-rights adjudication. Hantush (1965) extended this model to consider an imperfect hydraulic connection produced by clogging (siltation) at the interface between an aquifer and a fully penetrating stream (Figure 1b). This extension, however, has seen little use in practice.

Unfortunately, the idealized flow systems of Figure 1 bear little resemblance to many stream-aquifer systems. For example, streams in the Great Plains region of the United States commonly only partially penetrate through and are imperfectly connected with the adjoining aquifer. In many cases, the depth of stream penetration is a few tens of percent or less of the total aquifer thickness. Although not widely known in the United States, approximate analytical solutions have been developed that incorporate a simplified representation of partial penetration and an imperfect hydraulic connection (e.g., Grigoryev, 1957; Bochever, 1966). These solutions are based on a model (Figure 2) in which the degree of stream penetration is negligible relative to the aquifer thickness, and the stream is separated from the aquifer by a thin zone (the streambed) of relatively low hydraulic conductivity. Water movement across the low-conductivity stream bed is represented mathematically in the same manner as that used by Hantush and Jacob (1955) for modeling pumping-induced flow across an incompressible aquitard. Flow in the portions of the aquifer underneath the stream is confined, while that in the portions on either side of the stream is unconfined. The vertical component of flow is assumed to be very small, and the Dupuit assumptions are invoked to model flow in the aquifer.
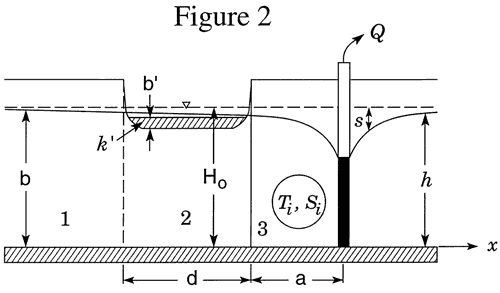
Recently, Zlotnik and Huang (1999) and Zlotnik et al. (1999) have extended this earlier work to develop specialized analytical solutions for consideration of floodwave propagation and stream depletion, respectively, in stream-aquifer systems that can be represented by Figure 2. Hunt (1999) has proposed a solution for pumping-induced drawdown and stream depletion using an infinitely thin stream variant of the model of Figure 2.
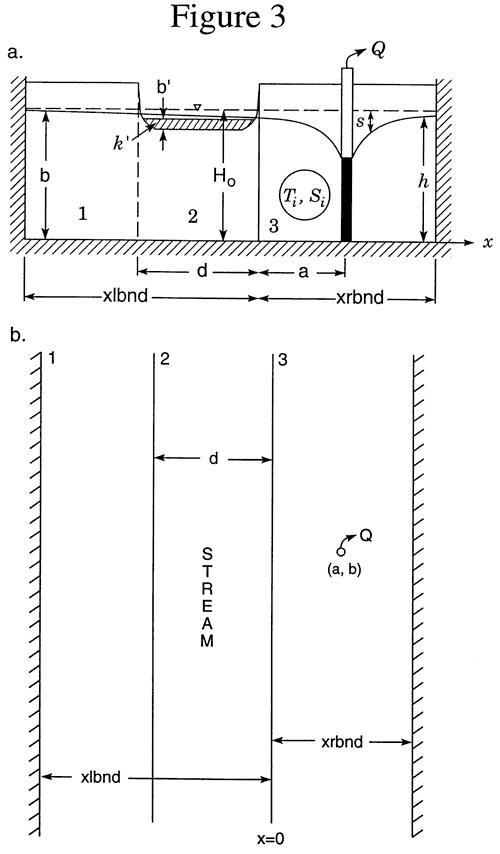
In this presentation, a more general semianalytical solution is presented. This solution can be utilized for computation of drawdown and stream depletion in both the infinitely wide aquifer of Figure 2, as well as the finite-width system of Figure 3. This solution will be used to assess the impact of finite stream width, shallow stream penetration, a low-permeability streambed, and a finite-width aquifer on pumping-induced drawdown and stream depletion. The solution will also help clarify where field efforts should be concentrated in order to improve the reliability of estimates of pumping-induced water transfers.
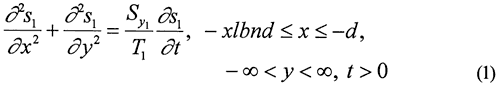
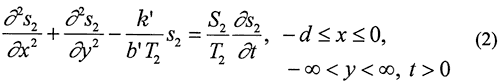
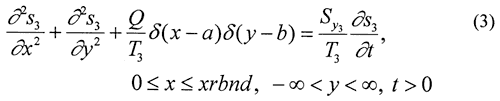
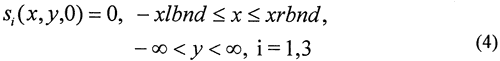
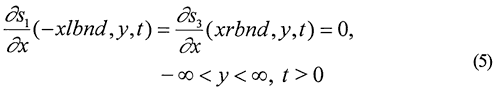
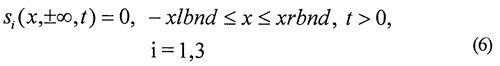
![]()
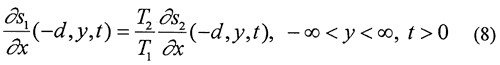
![]()
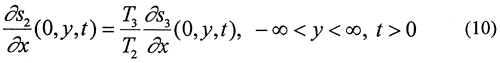
where
si = pumping-induced drawdown in zone i, [L];
Ti = transmissivity in zone i, [L2/T];
Syi and Si = specific yield or storativity of zone i, [dimensionless];
k' = hydraulic conductivity of streambed, [L/T];
b' = thickness of streambed, [L];
Q = pumpage from well at (a, b), [L3/T];
xlbnd, xrbnd = distance from right boundary of stream to left and right lateral boundary, respectively, [L];
d = width of stream, [L].
The mathematical model defined by (1)-(10) was solved using an approach analogous to that of Butler and Liu (1991). A series of integral transforms (Laplace transform in time and Fourier transform in the y direction) were applied to obtain functions in transform space that satisfy the transform-space analogues of (1)-(10). The inversion of the solution to real space was accomplished using Romberg integration (Carnahan et al., 1969) and the Stehfest (1970) algorithm for the Fourier and Laplace transforms, respectively.
The normalized stream depletion,
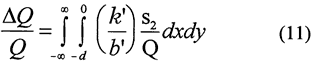
where ΔQ = pumping-induced flow from stream, [L3/T], was calculated, following the approach described by Hunt (1999), using the transform-space analogue of (11).
The approach described in the previous section was implemented using the StrpStrm program (Butler et al., 1999). The output of this program was compared to drawdown and stream depletion computed using a number of existing solutions. In this presentation, comparisons with stream depletion calculated using the solutions of Glover and Balmer (1954) and Hunt (1999) will be considered. In most of the following figures, dimensionless parameters will be utilized to increase the generality of the presented results. These dimensionless parameters are defined as follows:
α = a/d;
B (dimensionless stream leakance) = (k'd2)/(b'T2);
ξ = x/d;
XRB = xrbnd/d;
τ (dimensionless time)=(T3t)/(d2Sy3).
Figure 4 is a plot of normalized stream depletion (equation (11)) versus dimensionless time. As shown in the figure, the solution of Glover and Balmer (Figure 1a) can be reproduced with StrpStrm using a very large value for B (relatively large stream leakance). The comparison with the solution of Hunt (the Hunt leakance parameter, λD(=(k'da)/b'T2), is equivalent to B for this comparison) is not as good. As a result of the infinitely thin stream assumption invoked in the Hunt solution, the stream leakance is concentrated at x=O. Figure 4 shows that this can lead to an over-estimation of stream depletion when the stream leakance is large and/or the pumping well is relatively close to the stream. Drawdown (not shown here) computed with MODFLOW using the River and Well packages was in excellent agreement with that calculated using StrpStrm.
Figure 4. Comparison of stream depletion estimates obtained with Glover-Balmer, Hunt, and StrpStrm solutions.
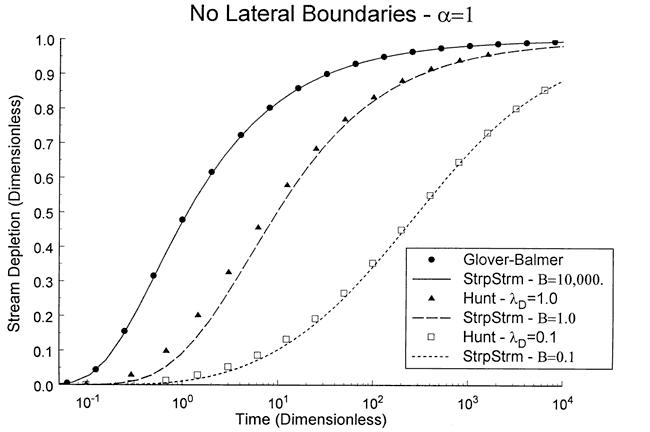
Figure 4 demonstrates that the dimensionless stream leakance (B) is an important control on stream depletion. In order to more systematically examine the dependence of drawdown and stream depletion on this parameter, a series of simulations were run in which B was varied over the range expected for most field applications.
Figure 5 is a dimensionless plot of drawdown versus time for an observation well at a distance of ξ=0.5 from the stream (pumping well at a distance of α=1 from the stream). In this case, a six order of magnitude variation in B spanned the range of drawdown behaviors that would be expected in the field. For B < 0.001, the drawdown is equal to that of the infinite-aquifer model of Theis (1935), i.e. the contribution of the stream is negligible. On the other hand, for B > 10,000, the drawdown is equal to that of the fully penetrating stream model of Theis (1941), i.e. the stream has a very significant contribution.
Figure 5. Dimensionless drawdown versus time.
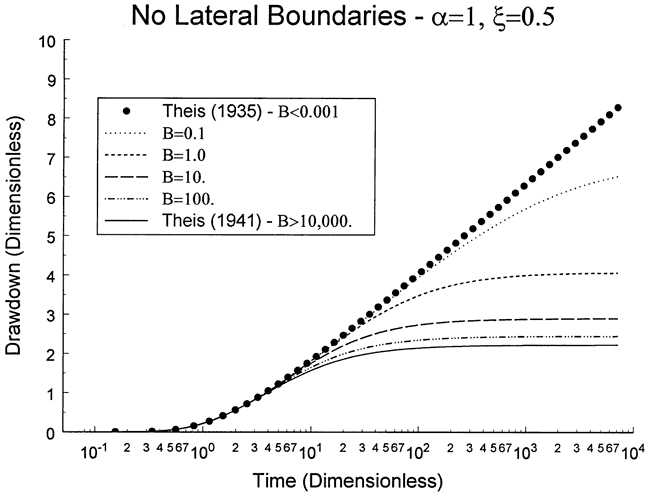
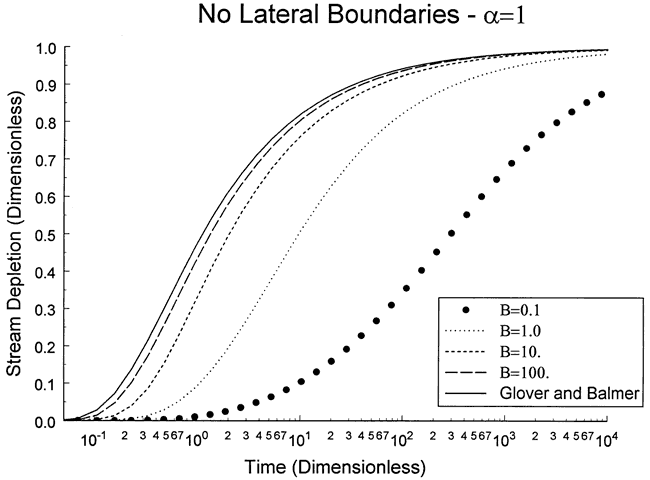
Figure 6 is a dimensionless plot of stream depletion versus time. As in Figure 5, increases in B lead to convergence on results from a model of a fully penetrating stream (Glover and Balmer, 1954). This figure demonstrates that use of a fully penetrating stream model may introduce considerable error when B is small. Clearly, the estimation of the quantities comprising the B parameter should be an important goal of field investigations.
Figure 6. Dimensionless stream depletion versus time.
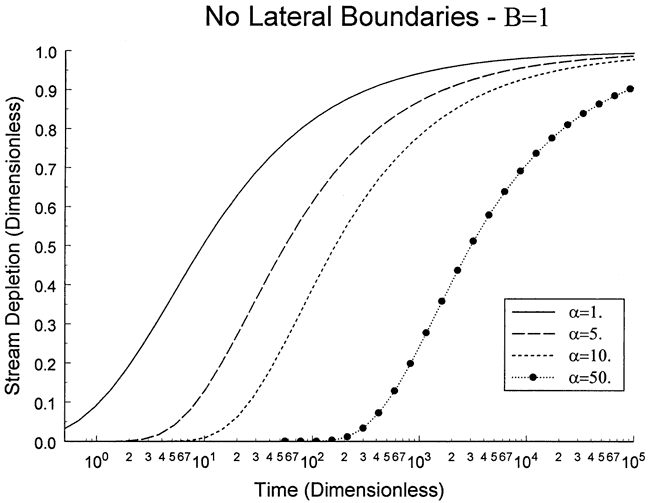
The stream-depletion curves shown in Figure 6 were calculated for a pumping well at a distance of α=1.0 from the stream. Figure 7 shows how stream depletion depends on the distance between the pumping well and the stream.
Figure 7. Dimensionless stream depletion versus time.
Dimensionless parameters are a convenient means to succinctly summarize the results generated with StrpStrm. Since stream width (d) is used as a normalizing quantity for length, it appears in most of the dimensionless parameters. Thus, it can be difficult to assess the dependence of drawdown and stream depletion on the width of the stream using dimensionless plots. The dependence on stream width can be more clearly demonstrated using simulation results presented in a dimensional form. In order to assess the dependence of stream depletion on stream width, a series of simulations were performed using the following parameters:
Ti = 200 m2/day;
Sy1 = Sy3 = 0.2;
S2 = 0.001;
a = 100 m;
Q = 1000 m3/day;
k' = 0.1 m/day;
b' = 0.1 m.
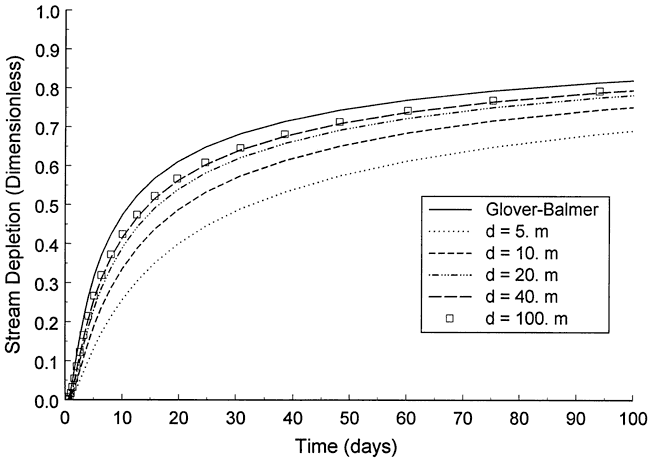
Figure 8 is a plot of dimensionless stream depletion versus time for a series of simulations using these parameters and varying the stream width between 5 and 100 meters (B=O.125-50, α=20-1). The Glover-Balmer solution is also shown for reference purposes. In this case, the curves do not converge on the Glover-Balmer solution as the stream width gets large. The computed stream depletion essentially does not change for stream widths greater than 30-40 meters. Zlotnik et al. (1999) state that this result is a product of increases in the length of the groundwater flow path under the stream limiting the effects of further increases in stream width.
Figure 8. Dependence of stream depletion estimates on stream width--no lateral boundaries.
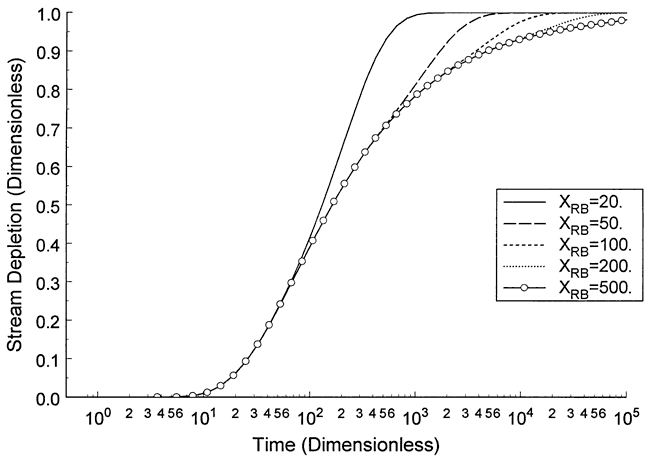
The previous figures were generated assuming that the aquifer can be considered laterally infinite (Figure 2) for the computation of drawdown and stream depletion. In order to assess the dependence of these quantities on the position of the lateral boundaries, an additional series of cases were considered in which the lateral boundaries were set at a finite distance from the stream (Figure 3).
Figure 9 displays the dependence of stream depletion on the distance to the lateral boundaries for the case of a stream at the exact center of the river valley. This figure shows that as the distance to the boundaries gets large relative to the distance between the pumping well and the stream (XRB/α > 20), the impact of the lateral boundaries becomes quite small. Although these results were obtained for a stream located at the center of the river valley, this dimensionless criterion is also appropriate for the case when the stream is not centrally located. In that case, however, the normalizing distance should be the distance to the closest lateral boundary, which can be on the opposite side of the stream from the pumping well. Since the stream channel may often be located against one side of the valley, the impact of lateral boundaries on stream depletion calculations can be of practical significance.Figure 9. Dimensionless streram depletion versus time dependence on laterall boundaries; B = 1, α = 10.
A new semianalytical solution has been developed for estimation of the drawdown and stream depletion produced by pumping from a well in the vicinity of a stream. This solution is based on a representation of the stream-aquifer interface that is more realistic than that employed in the commonly used analytical methods for estimation of pumping-induced water transfers. This solution can be utilized to assess the impact of finite stream width, shallow stream penetration, a low-permeability streambed, and a finite-width aquifer on drawdown and stream-depletion calculations. Results show that the dimensionless stream leakance parameter is a very important control on behavior in interconnected stream-aquifer systems. The assumption of an extremely large stream leakance, which underlies the commonly used methods, can lead to significant overestimations of stream depletion in many practical applications. Field investigations should therefore be focused on acquiring information about the quantities comprising this parameter. Although many of the commonly used methods assume that the aquifer is laterally infinite for stream-depletion calculations, the impact of lateral boundaries may often be of practical significance. Ongoing theoretical and field investigations are directed at extending this model and assessing the practical ramifications of these findings.
This research was supported by a grant from the Regional Water Resources Competitive Grants Program of the United States Geological Survey (USGS). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the USGS.
Bochever, F.M., 1966, Evaluation of well-field yield in alluvial aquifers: The impact of a partially penetrating stream: Proceedings of VODGEO (Hydrogeology), No. 13, 84-115, in Russian.
Butler, J.J., Jr., and W.Z., Liu, 1991, Pumping tests in non-uniform aquifers: The linear strip case: Jour. Hydrology, v. 128, p. 69-99.
Butler, J.J., Jr., Tsou, M.-S., and W.Z. Liu, 1999, The StrpStrm model for calculation of pumping-induced drawdown and stream depletion (version 1.0): Kansas Geological Survey, Computer Series Rept. 99-1.
Carnahan, B., Luther, H.A., and J.O. Wilkes, 1969, Applied Numerical Methods: John Wiley & Sons, Inc., New York, 604 pp.
Glover, R.E., and G.G. Balmer, 1954, River depletion resulting from pumping a well near a river: Am. Geophys. Union, Trans., v. 35, p. 468-470.
Grigoryev, V. M., 1957, The effect of streambed siltation on well-field yield in alluvial aquifers: Water Supply and Sanitation, No. 6, p. 110-118, in Russian.
Hantush, M.S., 1965. Wells near streams with semi-pervious beds: Jour. Geophys. Res., v. 70, no. 12, p. 2829-2838.
Hantush, M.S., and C.E. Jacob, 1955, Non-steady radial flow in an infinite leaky aquifer: Am. Geophys. Union, Trans., v. 36, no. 1, p. 95-100.
Hunt, B., 1999, Unsteady stream depletion from ground-water pumping: Ground Water, v. 37, no. 1, p. 98-102.
Jenkins, C. T., 1968, Techniques for computing rate and volume of stream depletion by wells: Ground Water, v. 6, no. 2, p. 37-46.
Stehfest, H., 1970, Numerical inversion of Laplace Transforms: Commun. ACM, v. 13, no. 1, p. 47-49.
Theis, C.V., 1935, The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage: Am. Geophys. Union, Trans., v. 16, no. 2, p. 519-524.
Theis, C.V., 1941, The effect of a well on the flow of a nearby stream: Am. Geophys. Union, Trans., v. 22, no. 3, p. 734-738.
Zlotnik, V.A., and H. Huang, 1999, Effect of partial penetration and streambed sediments on aquifer response to stream stage fluctuations, Ground Water, v. 37, no. 4, p. 599-605.
Zlotnik, V.A., Huang, H., and J.J. Butler, Jr., 1999, Evaluation of stream depletion considering finite stream width, shallow penetration, and properties of streambed sediments; in, Proc. of Water 99, Joint Congress, July 6-8, 1999, Brisbane, Australia, p. 221-226.
Kansas Geological Survey, Geohydrology
Placed online Nov. 28, 2007; original report dated June 1999
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Hydro/Publications/1999/OFR99_16/index.html